There are numerous systems in which it is of interest to study the flow of multiple fluids through porous media. Some examples of these include the transport of dissolved nutrients through biological tissue and the extraction of petroleum from underground deposits. In many practical situations, the physics of such flows are characterised by coupled governing equations that are nonlinear and transient, and the problem is further complicated by material heterogeneity and irregular geometries.
The goal of this work is to devise and implement general numerical algorithms for such systems. Our specific focus is on robustness through adaptive error-control and an implementation that’s readable by a normal human. (How many buzzwords can you cram into a sentence?)
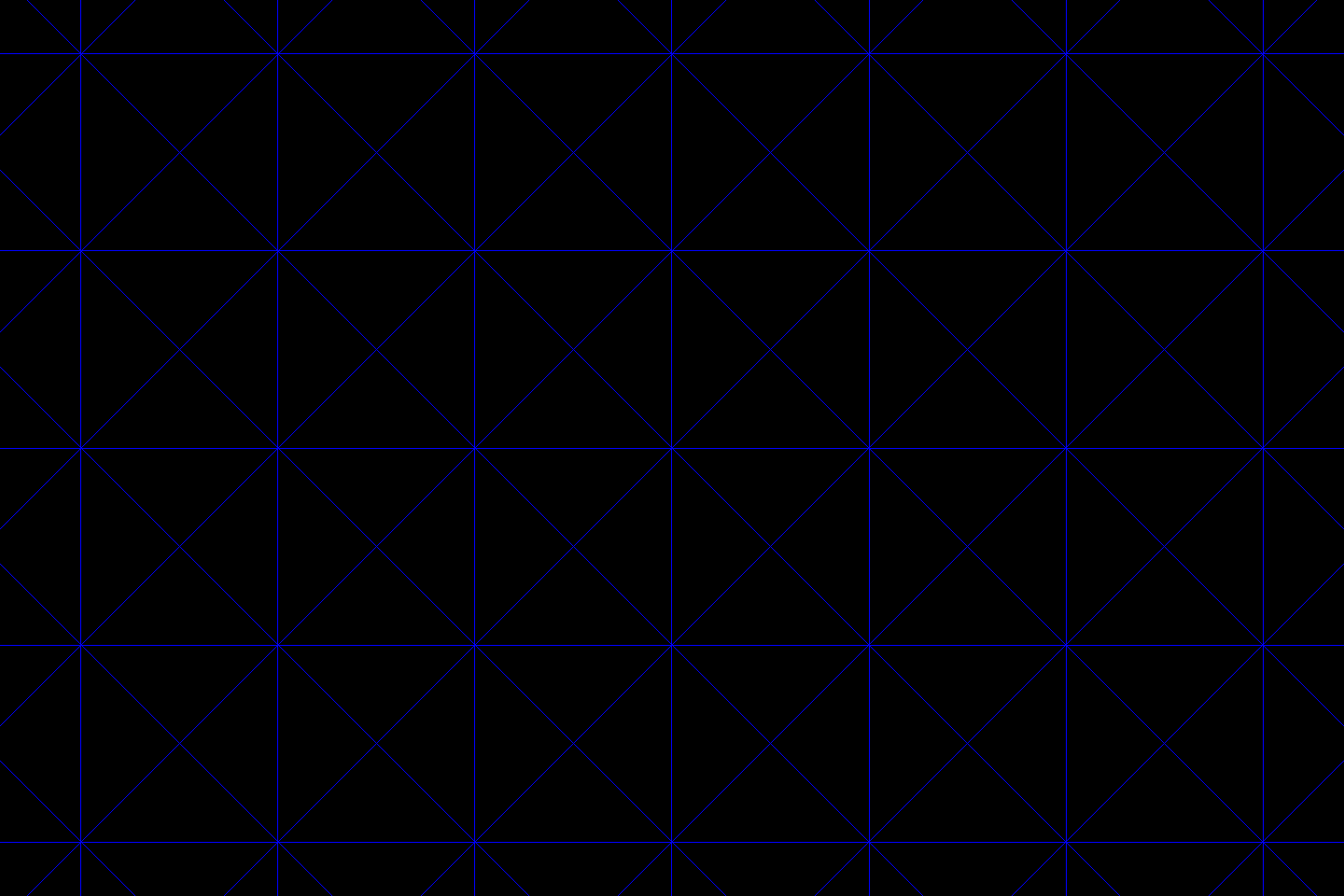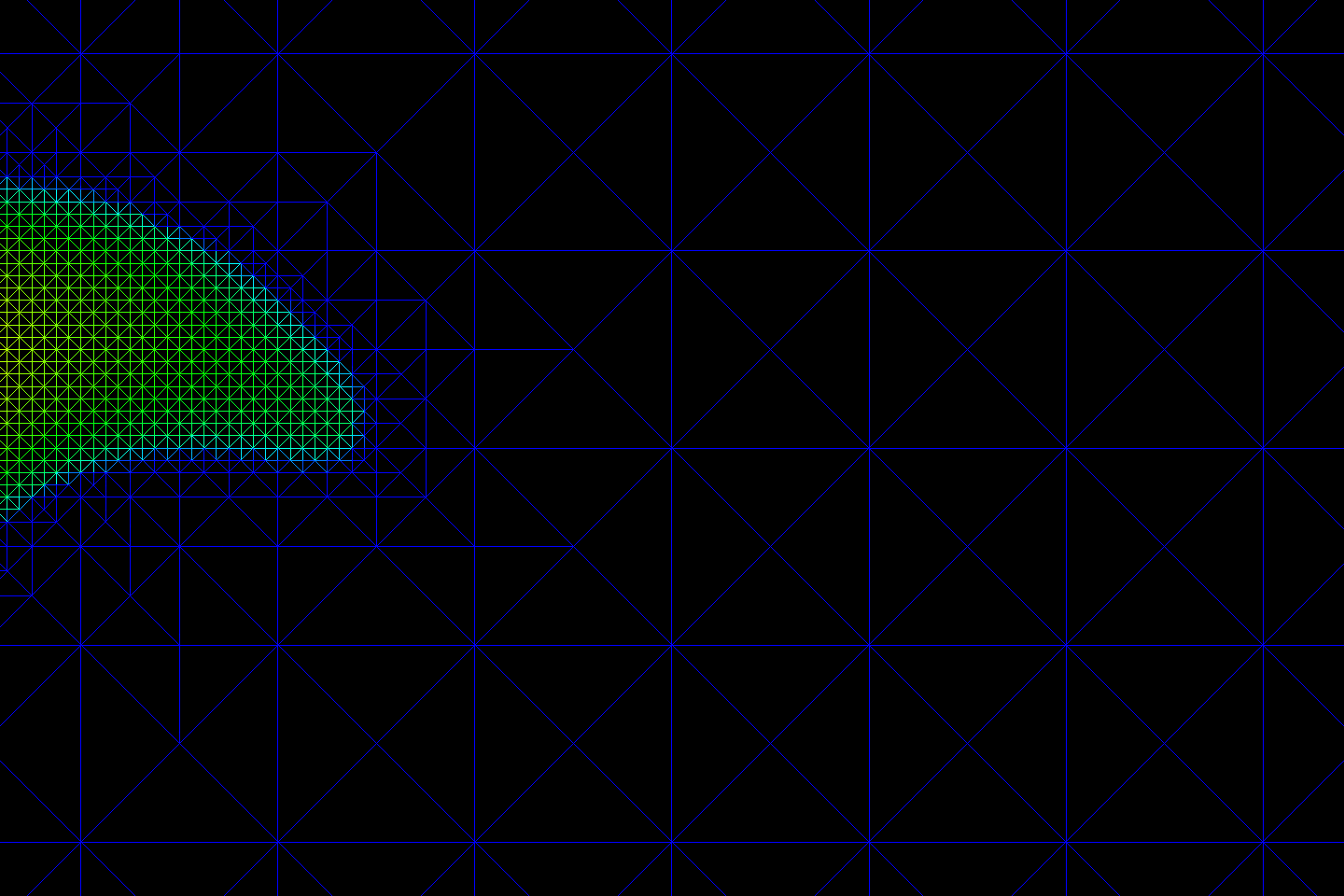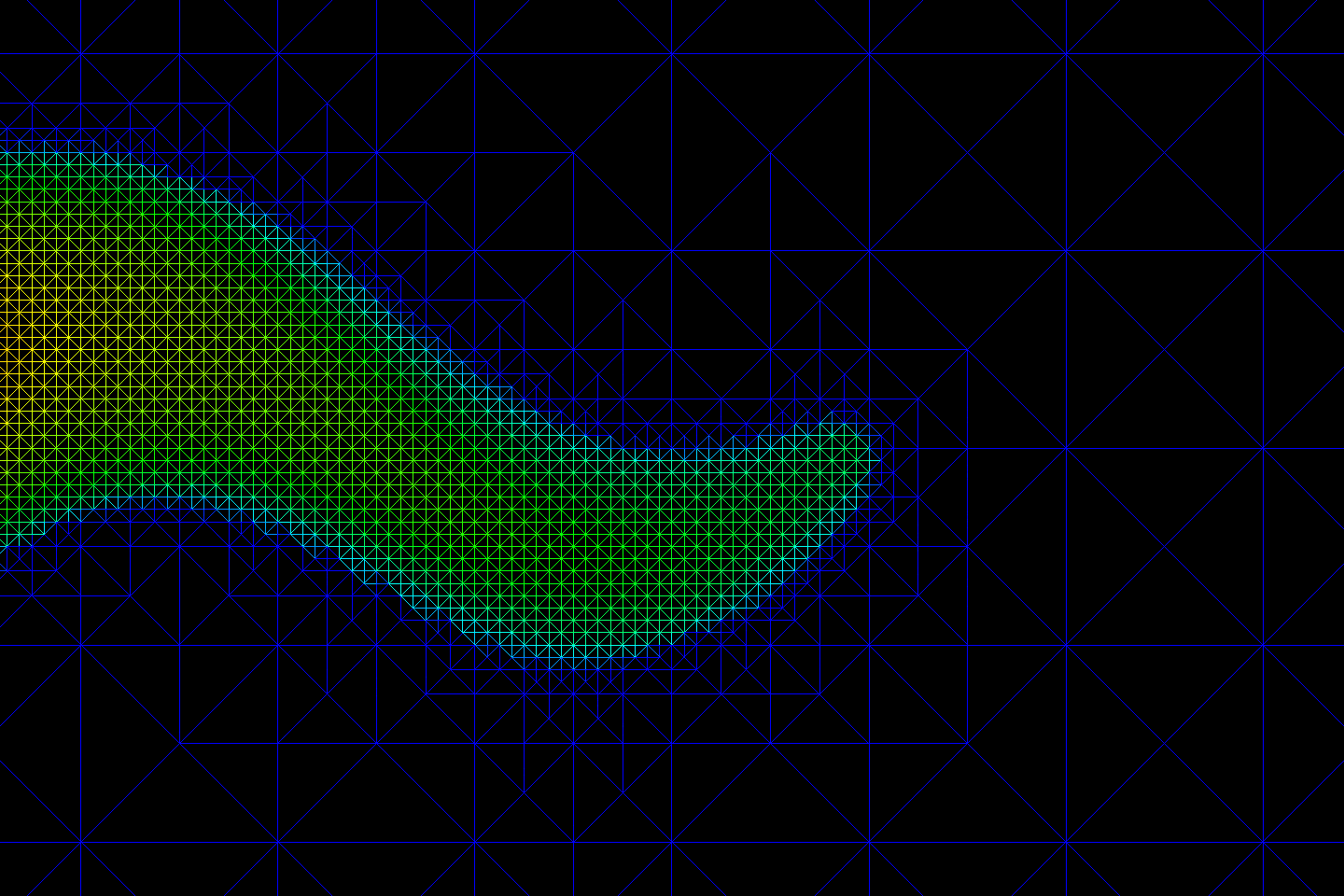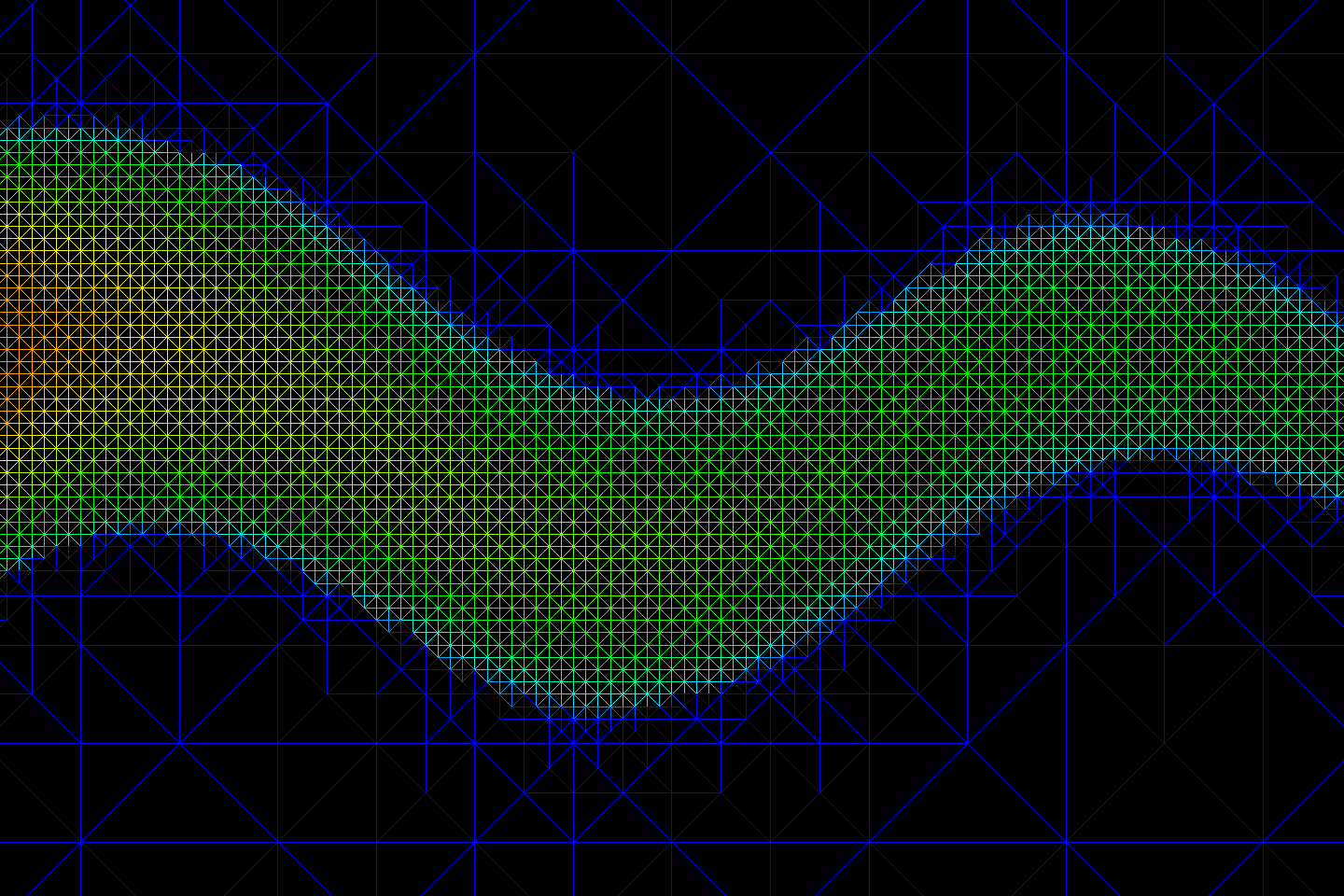
The following animation presents results from a simple (yet non-trivial!) calculation involving the flow of water and oil through fluid-saturated clay. The flow is driven from left to right by a pressure gradient. Because of the specific choice of a single, winding crack that snakes through the domain, it is in this high-permeability region that the greatest flow rates are set up. It is also in this region that the automatic methods most refine the computational mesh — ensuring that the fields we solve for are within specified numerical tolerances.
The model for the above example contains an elliptic equation and a
nonlinear hyperbolic transport equation. This system is solved at each
time-step using a mixed finite element formulation for the total
velocity, pressure and water saturation in the BDM(q) x DG(q - 1) x DG(q - 1) space. The Crank-Nicholson scheme is used for progressing
through time, and the mesh is adapted using a dual-weighted residual
strategy to concentrate the degrees of freedom in interesting parts of
the domain.
This research was carried out in collaboration with Garth N. Wells at the University of Cambridge from November 2009 to February 2010. The code for this effort comprises entirely of a few hundred lines of human-readable Python sitting atop the FEniCS Project. It is released as Free Software under the GNU GPL.