The following are some lessons learnt while implementing numerical methods for the Navier-Stokes equations.
A tale of two formulations
It is common in the literature to start with the Laplacian formulation of the Navier-Stokes equations,
\begin{align} \mathrm{div}(v) &= 0 \\ \rho \frac{\partial v}{\partial t} + \rho \left(\mathrm{grad}(v)\right)v &= -\mathrm{grad}(p) + \mu \mathrm{lap}(v), \end{align}
when going about deriving numerical methods to simulate incompressible viscous flow. When considered in this strong form, the above formulation is equivalent to the following divergence formulation arising from continuum mechanics:
\begin{align} \mathrm{div}(v) &= 0 \\ \rho \frac{\partial v}{\partial t} + \rho \left(\mathrm{grad}(v)\right)v &= \mathrm{div}(\sigma), \end{align}
where, for our Newtonian fluid, $\sigma = -p I\ + \mu \left(\mathrm{grad}(v) + \mathrm{grad}(v)^{T} \right)$.
Even though these two points of view are equivalent in the strong form, there are a few things one should keep in mind in practice. When integrated by parts to construct a weak form suitable for the finite element method, the two formulations above return different Neumann boundary terms. The divergence formulation introduces a boundary term with the traction, $\sigma n$, whereas the Laplacian formulation introduces a term with the normal derivative of the velocity, $\frac{\partial v}{\partial n}$. This means:
-
You probably want to pick the formulation based on the kind of boundary conditions you wish to impose. e.g., If you are considering a fully-developed channel flow, you know that there is a pressure and an (unknown, non-zero) shear stress at the outlet. Since you cannot set an unknown stress condition, the natural choice for this case is the Laplacian formulation with conditions $\frac{\partial v}{\partial n} = 0$ and $\int p = 0$. On the other hand, if you were considering free surface flow, you need to set the traction at the surface to a known value (usually 0). In this case, the divergence formulation is the logical choice.
-
You need to be aware of some subtleties involved in impementing the Laplacian formulation, or you may end up violating objectivity (as this formulation does not introduce the notion of a symmetric Cauchy stress).
-
In accordance with the formulation you choose, you must pay attention to how you implement boundary conditions. Otherwise you will (obviously) not see the flow you want.
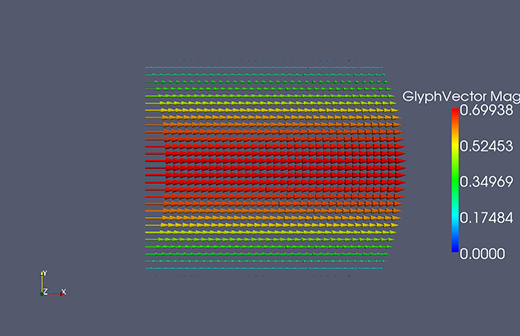
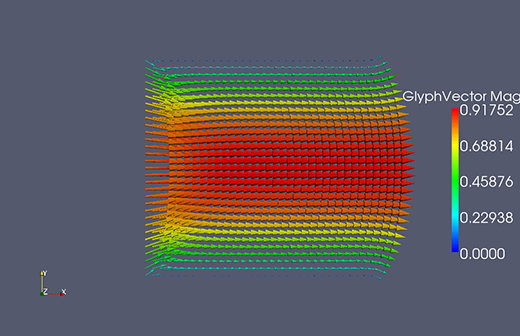
Some analytical solutions
The following are some analytical solutions for the Navier-Stokes equations, useful in benchmarking numerical algorithms.
- A 2D solution generated in Mathematica.
- A 3D solution generated in Mathematica.
- A SymPy script used to test analytical fluid-structure-interaction solutions.