This piece summarises aspects of the work that went into my Ph.D. dissertation. If you’re interested in more details, head on over to my more formal research writing.
Introduction
There is a lot of compelling clinical evidence that suggests the pervasive influence of mechanical factors in biological growth. The central goal of this modelling work is to gain a deeper understanding of the biophysical bases underlying these influences.
The utility of the resulting mathematical and computational framework extends across disciplines by helping steer and interpret experimental work, both under physiological and pathological cases of interest. Our initial focus is directed toward a better understanding of the mechanics of growing soft tissue, specifically tendon.

General formulation for growth in tissues
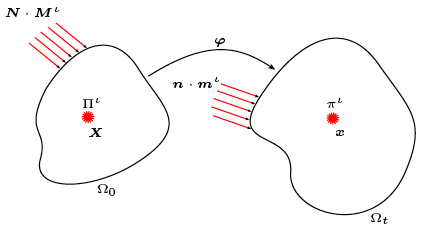
Growth in biological tissue is a direct outcome of cascades of complex, intracellular, biochemical reactions involving numerous species, their diffusion across cell membranes, and transport through the extra-cellular matrix. Both reaction and diffusion/transport are influenced by mechanics in a number of ways. Our modelling effort proposes a general continuum field formulation for growth capable of simulating this rich observed behaviour, and proceeds to specialise it incorporating different modelling assumptions—such as the use of an enzyme kinetics-based growth law—to better represent cases of interest.
Recognising that a growing tissue is an open system undergoing irreversible thermodynamics, the model incorporates the physics of multi-phase reacting systems, and deduces balance laws and a constitutive framework obeying the Second Law of Thermodynamics.
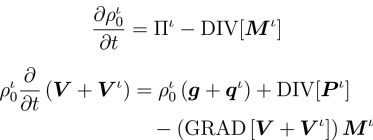
Notably, the transport of the extracellular fluid relative to the matrix is shown to be driven by the gradients of stress, concentration and chemical potential—a coupling of mass transport and mechanics that emerges directly.
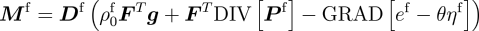
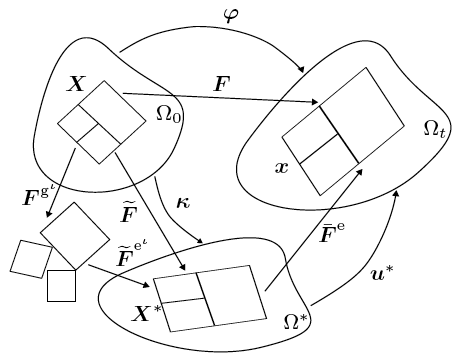
Assumptions central to existing mechanics theories, such as the nature of the split of deformation maps across the different species involved, and those on momentum transfers between interacting species, are revisited, analysed and carefully revised in cases where they limit the biophysical correctness of predicted growth phenomena.
Coupled, non-linear partial differential equations arise from the theory to describe the complex physics. These differential equations are solved using a finite element scheme based on operator-splits; incorporating non-linear projection methods to treat incompressibility, energy-momentum conserving algorithms for dynamics, and mixed methods for stress gradient-driven fluxes.
One highlight of the numerical methods is a rigorous treatment of numerical stability issues that arise with any operator-splitting scheme. This analysis is critical to the ability to distinguish physical instabilities, such as unbounded growth of tumours, from those that are artifacts of the numerical methods. Another key feature is the reformulation of the reaction-transport equations to embed the incompressibility constraint on the fluid phase, enabling a straightforward implementation of numerical stabilisation in the advection-dominated limit.

Mechanics of growing tissue
Using model geometries and imposing classes of initial and boundary conditions approximating experiments in our laboratory, the computational framework developed is used to demonstrate aspects of the coupled phenomena as the tissue grows. In these foundational calculations, only two phases—fluid and collagen—are included. The collagen phase is modelled by the anisotropic worm-like chain model, and the fluid phase is modelled as ideal and nearly incompressible. The interconversion between these two phases is modelled using first-order chemical kinetics.
For a tissue undergoing finite strains, the transport equations can be formulated, mathematically, in terms of quantities with respect to either the reference or current (deformed) configuration. However, the physics of fluid-tissue interactions, and the imposition of relevant boundary conditions, is best understood and represented in the current configuration.
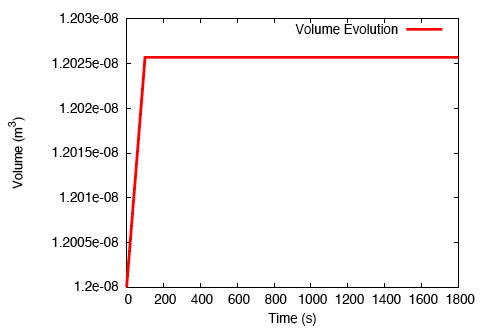
When a tendon having an initially-uniform distribution of collagen is immersed into a nutrient-rich bath, nutrient-rich fluid is transported into the tissue, and growth occurs due to the formation of additional collagen.

There is a rapid, fluid transport-dominated swelling of the tendon initially as it is immersed into the fluid bath. This is followed by a slower, reaction-driven growth phase.
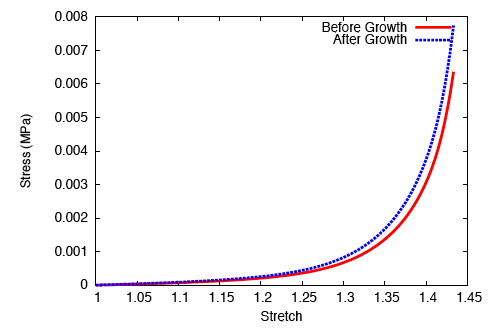
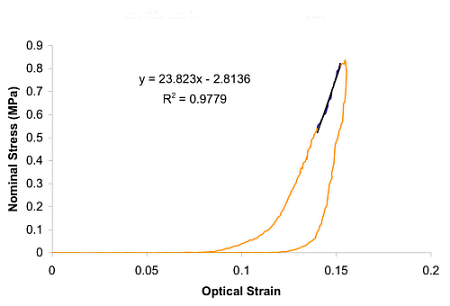
On performing a uniaxial tension test on the tendon before and after growth, it is observed that the grown tissue—having a higher concentration of collagen—is stiffer and stronger; which is in accordance with experiment.
Upon subjecting the tendon to a load-unload cycle, a stress-strain curve characteristic of viscoelastic tissue is observed. Here, the area between the loading and unloading paths is the hysteretic energy loss due to viscous dissipation.
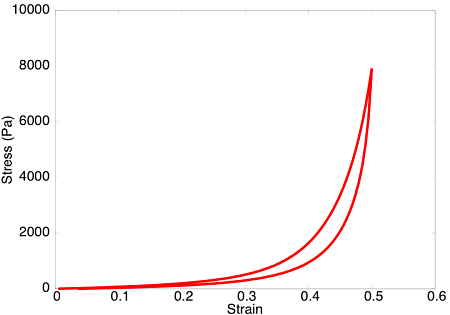
Qualitatively, this viscoelastic behaviour compares favourably with our corresponding experimental tests on two-week-old tibialis anterior tendons in the laboratory.
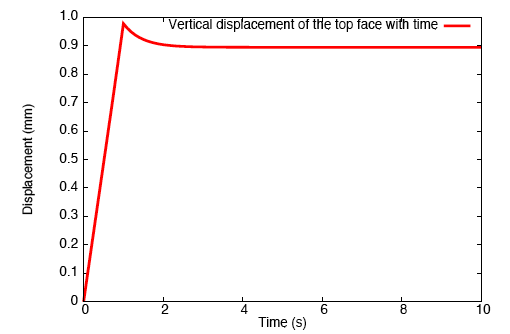
Application of a constrictive radial load—where the maximum strain in the radial direction is experienced half-way through the height of the tendon—to a tendon immersed in a fluid-filled bath results in a stress-gradient induced fluid flux. This drives fluid away from the central plane.

This pressure wave set up in the fluid travels toward the top and bottom faces, and as the fluid leaves these surfaces, we observe that the tendon relaxes.
Drug delivery and wound healing
Having established the fundamental behaviour of the formulation, we now turn to more sophisticated applications.
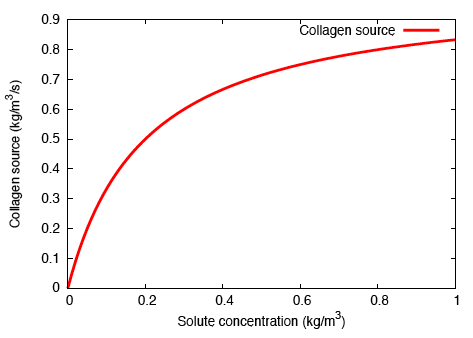
In order to model localised, bolus delivery of regulatory chemicals to the tendon while accounting for mechanical effects, we introduce additional species: a solute, and a distribution of fibroblasts that are characterised by their cell concentration. Both concentration gradient-driven mass transport and stress gradient-driven fluid flow are incorporated into this illustration, which demonstrates the use of the formulation in studying the efficacy of drug delivery mechanisms. Michaelis-Menten enzyme kinetics is used to determine the rates of solute consumption and, consequently, collagen production.

In addition to subjecting the tendon immersed in the bath to the constrictive radial load described earlier, a solute-rich bulb with its centre on the axis of the tendon is introduced. The relatively small magnitude of the fluid mobility—with respect to the diffusion coefficient for the solute through the fluid—results in a relatively small stress gradient-driven flux, and the transport of the solute is diffusion dominated. Consequently, as time progresses, the solute primarily diffuses locally, and as the solute concentration in a region increases, the enzyme-kinetics model predicts a small source term for collagen, and we observe nominal growth.
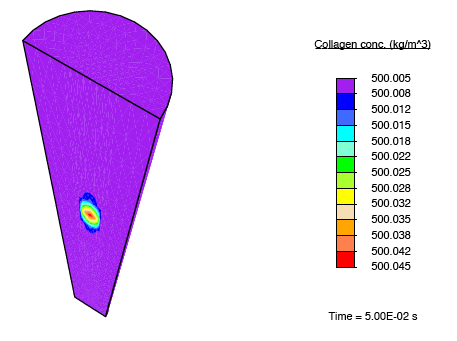
The following computation demonstrates the capability of the formulation in studying the self-healing of damaged tissue. Incorporating a cell-signalling parameter into the chemical kinetics, the formation of collagen is spatially biased toward damaged regions of the tissue.
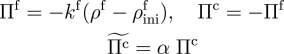
Turning to damaged skin as our tissue of interest, we begin by delineating the damaged regions—characterised by a sudden reduction in the concentration of collagen—from the rest of the tissue.

This damaged tissue is introduced to a nutrient-rich environment, and the cell-signalling parameter induces preferential growth in these damaged regions. We allow this healing process to evolve under two different conditions—under no load and under uniaxial stress—to study the influence of mechanics on the properties of healed tissue.
The anisotropic nature of these tissues arises from the microstructural alignment of their constituent collagen fibers, and the directionality of newly-deposited fibers are determined by the eigenvectors of the applied stress field. When the healing process is carried out under uniaxial stress, with the orientation of the stress being defined by the initially-stiff directionality of the tissue, the newly-deposited collagen has anisotropic properties which are identical to collagen in the undamaged tissue. This results in a healed tissue indistinguishable from the undamaged tissue.
However, when the healing process is carried out under no load, the newly-deposited collagen consists of arbitrarily-directed fibers, resulting in a formation of isotropic tissue in the damaged regions as the tissue heals. This results in a healed tissue being more compliant than the undamaged tissue along the originally-stiff direction of the tissue. Thus, upon being subjected to a load, these compliant healed regions experience a reduced stress.
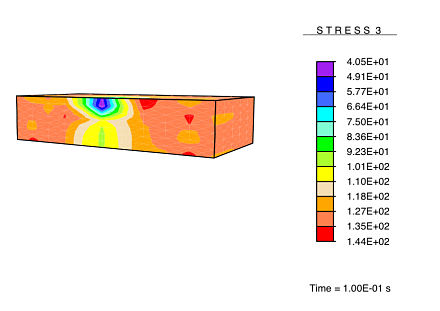
This result is analogous to the experimentally observed hypertrophic scarring of skin as it recovers from damage under no applied load.